Was bedeutet harmonikal ?

Spätestens seit Pythagoras (griechischer Mathematiker und Philosoph um 550 v.Chr.) beziehen Architekten die Prinzipien der musikalischen Harmonielehre in ihre Planungen mit ein. Eine musikalische Harmonie besteht aus mindestens zwei Tönen, die zusammen schwingen und dadurch einen Klang erzeugen. Verkürzt man die Saite eines Musikinstrumentes, beispielsweise einer Geige, durch Drücken mit einem Finger, so entstehen beim Niederdrücken der Saite nur an punktgenau bestimmbaren und sehr wenigen Stellen harmonische Zusammenklänge. Misst man die Entfernungen der Druckpunkte und setzt die ermittelten Maße untereinander in ein Verhältnis, entstehen immer ganzzahlige Brüche (z.B. 1/6, 2/3, 4/5). Es gibt auf unserer Erde verschiedene Musikkulturen, die unterschiedliche Zusammenklänge als besonders harmonisch erleben. Jedoch liegen allen diesen menschlichen musikalischen Systemen ganzzahlige Maßverhältnisse zugrunde.

Saitenlängen lassen sich sehr einfach in Tonhöhen (Frequenzen) umrechnen. Deshalb können harmonische Klänge (Frequenzen) durch die entsprechenden Maße (Saitenlängen) sichtbar gemacht werden. Harmonikal arbeitende Planer gehen davon aus, dass dadurch eine innere Harmonie in die so gestalteten Gebäude Einzug hält.

Die Quinte

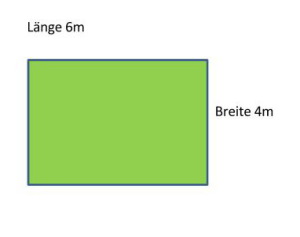
Als Beispiel sei an dieser Stelle das musikalische Intervall der Quinte erwähnt, das einzige Intervall, das tatsächlich von allen bekannten musikalischen Kulturen als besonders harmonisch bewertet wird. Wir stellen uns vor, wir hätten eine Geige mit zwei gleichen Saiten mit jeweils der Länge 30 cm. Beide Saiten erzeugen den gleichen Ton. Verkürzen wir eine der beiden Saiten um 10 cm auf 20 cm, so erhalten wir ein Saitenlängenverhältnis von 30:20, oder gekürzt von 3:2. Spielen wir beide Saiten gleichzeitig, so erhalten wir einen sehr harmonisch wirkenden Zusammenklang, den die Musiker Quinte nennen. Planen wir nun einen Raum, dessen eine Seite 30 cm und dessen andere Seite 20 cm lang ist, so haben wir ein harmonikales Abbild der Quinte architektonisch umgesetzt. Es hat sich herausgestellt, dass immer, wenn Saiten in diesem Verhältnis zueinander stehen, es zu dem Klangerlebnis „Quinte“ kommt. Alle Räume, deren beide Seitenlängen in diesem Maßverhältniss stehen, sind harmonisch. Ein Raum, der 6,00m lang und 4,00m breit ist, erfüllt dieses Kriterium. Räume haben natürlich mindestens auch noch eine Höhe. Ein einfacher quaderförmiger Raum stellt einen musikalischen Dreiklang architektonisch dar.

                                                                            Eine Quinte sichtbar gemacht :                          

Das Prinzip der Oktave

C-Dur ist die einsachste Tonart. Sie besteht aus den Tönen C D E F G A H C. Es fällt auf, dass Start- und Zielton jeweils ein C ist. Das hohe C ist aber nicht der gleiche Ton wie das tiefe C, trotzdem heißen beide Töne C. Spielt man beide Töne gleichzeitig, kann man sie praktisch nicht auseinanderhalten. Das hohe und das tiefe C schwingen im Verhältnis 2 : 1, die entsprechenden Saitenlängen stehen im Verhältnis 1 : 2 zueinander, also die Saitenlänge des tiefen C ist doppelt so lang wie die des hohen C. Halbieren wir die Saitenlänge, verdoppeln wir damit die Frequenz und es entsteht wieder der gleiche Ton, nur eine Oktave höher. Dieses Prinzip auf Maße angewendet bedeutet, dass 10 m das gleiche Prinzip verkörpert wie 20 m, oder 40 m oder 5 m, nur in einer anderen Oktave. Die Idee der Oktave ist eine wichtige Grundlage harmonikaler Planungen, wie auch eine unverzichtbare Basis der musikalischen Harmonielehre.

Wie aus Tönen Maße entstehen

Das Wort Harmonie beinhaltet immer, dass es mindestens zwei Elemente gibt, die zueinander in Harmonie stehen. Um von Harmonie zu reden, brauchen wir daher immer einen Bezugspunkt. In der Welt der Musik beziehen wir uns auf einen Grundton. Die anderen Töne werden zu diesem Grundton in Beziehung gesetzt. Nehmen wir wieder unsere C-Dur Tonleiter, so ist der Grundton C und alle anderen Töne stehen zu diesem Ton in einem bestimmten Schwingungs-Verhältnis:

Die Schwingungsfrequenz des Tones C steht zur Schwingungsfrequenz des Tones D im Verhältniss 8 : 9.  Es ergibt sich folgende Tabelle:

Tabelle für die Schwingungsfrequenz-Verhältnisse der C-Dur Tonleiter

Die Saitenlängen verhalten sich genau umgekehrt- Angenommen der Grundton C klingt auf einer Saite mit der Länge von 120 cm, hat der Ton D die Saitenlänge 120,00 cm x 8 : 9 = 106,70 cm.

Tabelle für die Saitenlängen der C-Dur Tonleiter bei einer angenommenen Saitenlänge von 120,00 cm

Die Saitenlängen der C-Dur Tonleiter sind also 120,00 cm, 106,70 cm, 96,00 cm, 90,00 cm, 80,00 cm, 72,00 cm, 64,00 cm und 60,00 cm. Dazu kommen alle Oktaven dieser Maße, also alle Maße beliebig oft mit 2 multipliziert oder durch 2 diviediert. Würden wir ein Gebäude ausschließlich mit diesen Maßen bauen, entstünde ein C-Dur Gebäude. In der Praxis reicht das jedoch nicht aus, es ist notwendig andere harmonische Maße mit einzubeziehen. Nimmt man auch Harmonielehren anderer Kulturen hinzu, so kann ein harmonikal geplantes Gebäude eine ganz spezielle multi-kulti-Tonart repräsentieren, die es vielleicht in keiner Musik der Welt gibt. Vielleicht findet sich ja dann ein Komponist, der zur Einweihung ein Werk in genau dieser Tonart erschafft?

Das Grundmaß

So wie für eine Musik ein Grundton gebraucht wird, so ist die erste Frage, die sich bei einer harmonikalen Planung stellt, die Frage nach dem Grundmaß. Tatsächlich haben wichtige Gebäude oft ein ganz eigenes Grundmaß. Als Beispiel sei hier die Elle von Chartres genannt. Spannend in diesem Zusammenhang ist ein Blick in die Vergangenheit der menschlichen Kulturen und deren Maßsysteme. Egal, ob wir Griechische, Ägyptische, Römische oder Hebräische Ellen oder Füße nehmen, all diese Maße sind ganzzahlige Teile unserer Erdmaße. Ein Beispiel: Der Griechische Fuß ist der mittlere Erdumfang 15 mal oktaviert (durch zwei geteilt), 5 mal durch 3 geteilt, dreimal durch 5 geteilt und einmal durch 11 geteilt. Damit steht der griechische Fuß harmonikal zum mittleren Erdumfang. Unser neues Maßsystem legt den Meter zugrunde. Der Meter hätte ein 40 Millionstel des Erdumfanges sein sollen. Der Erdumfang beträgt aber nicht 40.000.000 m, sondern 40.045.000 m. Die Differenz beträgt 45 km Eine solch große Abweichung gibt es bei keinem alten Maßsystem, so dass wir sagen können, dass das Meter das einzige nicht-harmonikale Maßsystem ist, das je auf der Erde in großem Umfang angewendet wurde. Wenn die Kulturen der Welt einen solch großen Wert auf den harmonikalen Charakter ihrer Maßsysteme legten, dann könnte es sich lohnen bei architektonischen Planungen diesen Aspekt zu berücksichtigen.

Das Grundmaß des Ippinger Riesen

Der Ippinger Riese ist ein Gebäude des Mittelalters, das wegen seiner hervorragen geomantischen Lage (Siehe Kapitel „Kraftort“) eine wichtige Bedeutung gehabt haben könnte. Die Jahrhunderte haben das Gebäude gezeichnet, so dass heute kein genauer rechteckiger Grundriss mehr vorhanden ist. Die ungefähren Grundrissmaße betragen knapp 39 m x knapp 16 m. In der Musik ist der tiefste Ton oftmals der Grundton, so dass die knappen 39 m als Grundmaß in Frage kommen.

Auf der Suche nach einem passenden Grundmaß fand sich die Wellenlänge des Merkurjahres. Der Merkur ist der sagenhafte Götterbote und steht für Kommunikation.

Legt man die Dauer des Merkurjahres mit 87,969 Tage zugrunde, so erhält man eine Frequenz von einer Schwingung in 87,969 Tagen. Diese Schwingung 26 mal oktaviert ergibt eine Frequenz von 8,8295 Hz. Das hört sich zunächst recht weit hergeholt an, doch hat schon ein normales Klavier einen Tonumfang von mehr als 7 Oktaven. Der Frequenzbereich, den das menschliche Ohr wahrnimmt umfasst mehr als 12 Oktaven.

Die Wellenlänge errechnet sich, indem man die Schallgeschwindigkeit von 343,2 m/s durch die Frequenz teilt, also 343,2 m/s : 8,8295 Hz = 38,87 m.

Der harmonikalen Planung wurde demnach ein Grundmaß von 38,87 m zugrunde gelegt, was der tatsächlichen Länge des Gebäudes entspricht. Die Länge steht im Verhältnis zur Breite wie die große Terz, also im Verhältnis 5 : 4, wobei die Länge oktaviert, d.h. verdoppelt wird. Daraus ergibt sich rechnerisch eine Gebäudebreite von 15,55 m, was ebenfalls der Realität entspricht.

Es ist kaum denkbar, dass die Baumeister des Ippinger Riesen bewußt das Merkurjahr als Grundfrequenz gewählt haben, denn dazu hätten sie sowohl die Schallgeschwindigkeit, als auch die genaue Dauer des Merkurjahres kennen müssen. Anzunehmen ist, dass das Grundmaß mit Bedacht gewählt wurde, wie aber ein Maß entstanden ist, das dem Merkurjahr entspricht, ist heute nicht mehr nachvollziehbar.

Harmonikale Detailplanung am Beispiel des Studios:

Die Grundfläche des Raumes: 9,72 m x 7,78 m, entspricht den Tönen C und E. Damit hat das Studio die gleiche Harmonie wie das Gesamtgebäude, nur jeweils oktaviert. Die Raumhöhe entspricht mit 5,19 m dem Ton H, so dass der Dreiklang C E H entsteht. Ein Dreiklang, wie er gerne im Jazz benutzt wird. Die Raumhöhen der Empore und des Bades, sowie unterhalb der Empore repräsentieren wieder den Ton C und messen daher 243 cm. Durch den Einbau des Bades ergeben sich noch zwei zusätzliche Maße: Von der südwestlichen Außenwand zum Bad ergeben sich 6,93 m, was dem Ton Fis entspricht. Unter der Empore entsteht so der Dreiklang E Fis C, ein Vorhaltakkord. Zwischen der Badwand und der Trennwand zum Nachbarzimmer  gibt es das Maß 3,08 m, als Ton wäre das ein As. Das Bad selber hat die Innenmaße 4,62 m Cis und 2,74 B. Zusammen mit der Raumhöhe ergibt sich wieder ein Vorhaltsklang: Cis B C. Es fällt auf, dass keine reinen Dur- oder Mollakkorde entstanden sind. Das ist auch nicht beabsichtigt, denn Räume sollen durchaus eine gewisse spannende Energie haben, nur sollte diese Energie auf harmonischen Füßen stehen. Weiterhin sind die Fenstermaße mit 108 cm x 216 cm, bzw 108 cm x 162 cm mit den Tönen D und G verbunden, was zusammen mit der Raumhöhe den Dreiklang H D G ergibt.

Durch die Realisierung der harmonikalen Planungsprinzipien ergibt sich ein angenehmes Raumgefühl und eine schöne Raumakkustik.

Im Zusammenspiel mit den biologischen Baustoffen und der Energetik des Platzes entsteht eine ganz besondere Atmosphäre.